Difference between revisions of "Fast Fourier Transform"
From Hydrogenaudio Knowledgebase
(category) |
|||
| Line 1: | Line 1: | ||
| + | {{stub}} | ||
| + | |||
| + | |||
Fast Fourier Transform is an efficient algorithm for calculating the discrete fourier transform ([[DFT]]). Reduces the execution time by hundreds in some cases. Whereas [[DFT]] takes an order of <math>O(n^2)\,</math> computations, FFT takes an order of <math>O(n\,\log\,n)</math>, and is definitely the preferred algorithm to used in all applications. The FFT in most implementations consistent of samples that are exactly a power of 2. | Fast Fourier Transform is an efficient algorithm for calculating the discrete fourier transform ([[DFT]]). Reduces the execution time by hundreds in some cases. Whereas [[DFT]] takes an order of <math>O(n^2)\,</math> computations, FFT takes an order of <math>O(n\,\log\,n)</math>, and is definitely the preferred algorithm to used in all applications. The FFT in most implementations consistent of samples that are exactly a power of 2. | ||
[[Category:Technical]] | [[Category:Technical]] | ||
| + | [[Category:Algorithm]] | ||
Revision as of 19:31, 5 September 2006
This article is a stub. You can help the Hydrogenaudio Knowledgebase by expanding it.
Fast Fourier Transform is an efficient algorithm for calculating the discrete fourier transform (DFT). Reduces the execution time by hundreds in some cases. Whereas DFT takes an order of 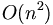 computations, FFT takes an order of
computations, FFT takes an order of 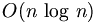 , and is definitely the preferred algorithm to used in all applications. The FFT in most implementations consistent of samples that are exactly a power of 2.
, and is definitely the preferred algorithm to used in all applications. The FFT in most implementations consistent of samples that are exactly a power of 2.