The MPEG-1 Layer III format

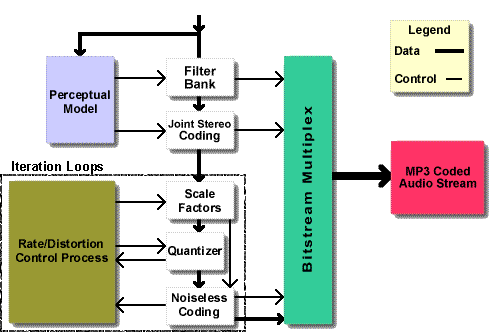
A basic functional block diagram of the MPEG1 layer 3 audio codec is as shown below.

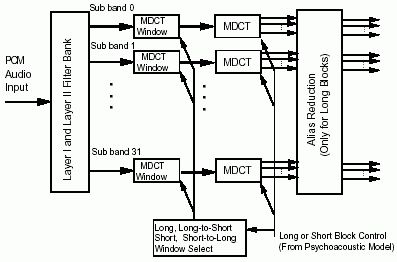
The Hybrid Polyphase FilterBank

The polyphase filterbank is the key component common to all layers of MPEG1 audio compression. The purpose of the polyphase filterbank is to divide the audio signal into 32 equal-width frequency subbands, by using a set of bandpass filters covering the entire audio frequency range (a set of 512 tap FIR Filters).

PolyphaseFilterbankFormula

Audio is processsed by frames of 1152 samples per audio channel. The polyphase filter groups 3 groups of 12 samples (3x12=36) samples per subband as seen from the picture above (3x12x32 subbands=1152 samples).

The polyphase filter bank and its inverse are not lossless transformations. Even without quantization, the inverse transformation cannot perfectly recover the original signal. However by design the error introduced by the filter bank is small and inaudible.

MDCT formula:

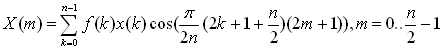
Layer 3 compensates for some of the filter bank deficiencies by processing the filter bank output with a Modified Discrete Cosine Transform (MDCT). The polyphase filterbank and the MDCT are together called as the Hybrid filterbank. The Hybrid FilterBank adapts to the signal characteristics (block switching depending on the signal etc.).

The 32 subband signals are subdivided further in frequency content by applying a 18-spectral point or 6-spectral point MDCT. Layer 3 specifies two different MDCT block lenghts: a long block (18 spectral points) or a short block (6 spectral points).

Long Blocks: Long blocks have a higher frequency resolution. Each subband is transformed into 18 spectral coefficients by MDCT, yielding a maximum of 576 spectral coefficients (32x18=576 spectral lines) each representing a bandwidth of 41.67Hz at 48kHz sampling rate. At 48kHz sampling rate a long block has a time resolution of about x ms. There is a 50% overlap between successive transform windows, so the window size is 36 for long blocks.

Short Blocks: Short blocks have a higher time resolution. Short block length is one third of a long block and used for transients to provide better time (temporal) resolution. Each subband is transformed into 6 spectral coefficients by MDCT, yielding a maximum of 192 spectral coefficients (32x6=192 spectral lines) each representing a bandwidth of 125Hz at 48kHz sampling rate. At 48kHz sampling rate a short block has impulse response of 18.6ms. There is a 50% overlap between successive transform windows, so the window size is 12 for short blocks.

Time resolutions of long blocks and time resolution of short blocks are not constants, but jitter depending on the position of the sample in the transformed block. See here for diagrams showing the average time resolutions of different codecs.

Block switching (MDCT window switching) is triggered by psycho acoustics.

For a given frame of 1152 samples, the MDCT's can all have the same block length (long or short) or have a mixed-block mode (mixed-block mode for Lame is in development).

Unlike only the polyphase filterbank, without quantization the MDCT transformation is lossless.

Once the MDCT converts the audio signal into the frequency domain, the aliasing introduced by the subsampling in the filterbank can be partially cancelled. The decoder has to undo this so that the inverse MDCT can reconstruct the subband samples in their original aliased form for reconstruction by the synthesis filterbank.

The Psychoacoustic model:(gathering data, incomplete)

Critical bands

Much of what is done in Simultaneous masking is based on the existence of critical bands. The hearing works much like a non-uniform filterbank, and the critical bands can be said to approximate the characteristics of those filters. Critical bands does not really have specific "on" and "off" frequencies, but rather width as a function of frequency - critical bandwidths.

Tonality estimation

Spreading function

Masking does not only occur within the critical band, but also spreads to neighboring bands. A spreading function SF(z,a) can be defined, where z is the frequency and a the amplitude of a masker. This function would give a masking threshold produced by a single masker for neighboring frequencies. The simplest function would be a triangular function with slopes of +25 and -10 dB / Bark, but a more sophisticated one is highly nonlinear and depends on both frequency and amplitude of masker.

Simultaneous masking

Simultaneous masking is a frequency domain phenomenon where a low level signal, e.g, a smallband noise (the maskee) can be made inaudible by simultaneously occuring stronger signal (the masker), e.g, a pure tone,if masker and maskee are close enough to each other in frequency. A masking threshold can be measured below which any signal will not be audible. The masking threshold depends on the sound pressure level (SPL) and the frequency of the masker, and on the characteristics of the masker and maskee. The slope of the masking threshold is steeper towards lower frequencies,i.e., higher frequencies are more easily masked.

Without a masker, a signal is inaudible if its SPL is below the threshold of quiet, which depends on frequency and covers a dynamic range of more than 60 dB. We have just described masking by only one masker. If the source signal consists of many simultaneous maskers, a global masking threshold can be computed that describes the threshold of just noticeable distortions as a function of frequency. The calculation of the global masking threshold is based on the high resolution short term amplitude spectrum of the audio or speech signal, sufficient for critical band based analysis, and is determined in audio coding via 512 or 1024 point FFT. In a first step all individual masking thresholds are calculated, depending on signal level, type of masker(noise or tone), and frequency range. Next the global masking threshold is determined by adding all individual thresholds and the threshold in quiet (adding this later threshold ensures that the computed global masking threshold is not below the threshold in quiet). The effects of masking reaching over critical band bounds must be included in the calculation. Finally the global signal-to-mask ratio (SMR) is determined as the ratio of the maximum of signal power and global masking threshold.

Temporal

In addition to simultaneous masking two time domain phenomena also play an important role in human auditory perception, pre-masking and post-masking. The temporal masking effects occur before and after a masking signal has been switched on and off, respectively. The duration when pre-masking applies is less than -or as newer results indicate, significantly less than-one tenth that of the post-masking, which is in the order of 50 to 200 msec. Both pre and post-masking are being exploited in the ISO/MPEG audio coding algorithm.

It uses either a separate filterbank or combines the calculation of energy values (for the masking calculations) and the main filter bank. The output of the perceptual model consists of values for the masking threshold or the allowed noise for each coder partition. If the quantization noise can be kept below the masking threshold, then the compression results should be indistinguishable from the original signal.

ATH

Masking threshold

Masking raises the threshold of hearing, and compressors take advantage of this effect by raising the noise floor, which allows the audio waveform to be expressed with fewer bits. The noise floor can only be raised at frequencies at which there is effective masking.

The equal widths of the subbands do not accurately reflect the human auditory system's frequency dependent behavior. The width of a "critical band" as a function of frequency is a good indicator of this behavior. Many psychoacoustic effects are consistent with a critical band frequency scaling. For example, both the perceived loudness of a signal and its audibility in the presence of a masking signal is different for signals within one critical band than for signals that extend over more than one critical band. Figure 2 compares the polyphase filter bandwidths with the width of these critical bands. At lower frequencies a single subband covers several critical bands.

The MPEG/audio algorithm compresses the audio data in large part by removing the acoustically irrelevant parts of the audio signal. That is, it takes advantage of the human auditory system's inability to hear quantization noise under conditions of auditory masking. This masking is a perceptual property of the human auditory system that occurs whenever the presence of a strong audio signal makes a temporal or spectral neighborhood of weaker audio signals imperceptible. A variety of psychoacoustic experiments corroborate this masking phenomenon[13].

Empirical results also show that the human auditory system has a limited, frequency dependent, resolution. This frequency dependency can be expressed in terms of critical band widths which are less than 100Hz for the lowest audible frequencies and more than 4kHz at the highest. The human auditory system blurs the various signal components within a critical band although this system's frequency selectivity is much finer than a critical band.

The psychoacoustic model analyzes the audio signal and computes the amount of noise masking available as a function of frequency ,14,15,16,17. The masking ability of a given signal component depends on its frequency position and its loudness. The encoder uses this information to decide how best to represent the input audio signal with its limited number of code bits. The MPEG/audio standard provides two example implementations of the psychoacoustic model.

Below is a general outline of the basic steps involved in the psychoacoustic calculations for either model. Differences between the two models will be highlighted.
- Time align audio data. There is one psychoacoustic evaluation per frame. The audio data sent to the psychoacoustic model must be concurrent with the audio data to be coded. The psychoacoustic model must account for both the delay of the audio data through the filterbank and a data offset so that the relevant data is centered within the psychoacoustic analysis window.
- Convert audio to a frequency domain representation. The psychoacoustic model should use a separate, independent, timeto- frequency mapping instead of the polyphase filter bank because it needs finer frequency resolution for an accurate calculation of the masking thresholds.

Layer II and III use a 1,152 sample frame size so the 1,024 sample window does not provide complete coverage. While ideally the analysis window should completely cover the samples to be coded, a 1,024 sample window is a reasonable compromise. Samples falling outside the analysis window generally will not have a major impact on the psychoacoustic evaluation.

For Layers II and III, the model computes two 1,024 point psychoacoustic calculations for each frame. The first calculation centers the first half of the 1,152 samples in the analysis window and the second calculation centers the second half. The model combines the results of the two calculations by using the higher of the two signal-to-mask ratios for each subband. This in effect selects the lower of the two noise masking thresholds for each subband.
- Process spectral values in groupings related to critical band widths. To simplify the psychoacoustic calculations, both models process the frequency values in perceptual quanta.

Psychoacoustic model 2 never actually separates tonal and non-tonal components. Instead, it computes a tonality index as a function of frequency. This index gives a measure of whether the component is more tone-like or noise-like. Model 2 uses this index to interpolate between pure tone-masking-noise and noise-masking-tone values. The tonality index is based on a measure of predictability. Model 2 uses data from the previous two analysis windows to predict, via linear extrapolation, the component values for the current window. Tonal components are more predictable and thus will have higher tonality indices. Because this process relies on more data, it is more likely to better discriminate between tonal and non-tonal components than the model 1 method.
- Apply a spreading function. The masking ability of a given signal spreads across its surrounding critical band. The model determines the noise masking thresholds by first applying an empirically determined masking (model 1) or spreading function (model 2) to the signal components.
- Set a lower bound for the threshold values. Both models include an empirically determined absolute masking threshold, the threshold in quiet. This threshold is the lower bound on the audibility of sound.
- Find the masking threshold for each subband. Model 2 selects the minimum of the masking thresholds covered by the subband only where the band is wide relative to the critical band in that frequency region. It uses the average of the masking thresholds covered by the subband where the band is narrow relative to the critical band. Model 2 is not less accurate for the higher frequency subbands because it does not concentrate the non-tonal components.
- Calculate the signal-to-mask ratio. The psychoacoustic model computes the signal-to-mask ratio as the ratio of the signal energy within the subband (or, for Layer III , a group of bands) to the minimum masking threshold for that subband. The model passes this value to the bit (or noise) allocation section of the encoder.
  - 2.1.1.1 Example for Psychoacoustic Model 2 The processes used by psychoacoustic model 2 are somewhat easier to visualize, so this model will be covered first. Figure 12a shows the result, according to psychoacoustic model 2, of transforming the audio signal to the perceptual domain (63, one-third critical band, partitions) and then applying the spreading function. Note the shift of the sinusoid peak and the expansion of the lowpass noise distribution. The perceptual transformation expands the low frequency region and compresses the higher frequency region. Because the spreading function is applied in a perceptual domain, the shape of the spreading function is relatively uniform as a function of partition. Figure 13 shows a plot of the spreading functions. Figure 12b shows the tonality index for the audio signal as computed by psychoacoustic model 2. Figure 14a shows a plot of the masking threshold as computed by the model based on the spread energy and the tonality index. This figure has plots of the masking threshold both before and after the incorporation of the threshold in quiet to illustrate its impact. Note the threshold in quiet significantly increases the noise masking threshold for the higher frequencies. The human auditory system is much less sensitive in this region. Also note how the sinusoid signal increases the masking threshold for the neighboring frequencies. The masking threshold is computed in the uniform frequency domain instead of the perceptual domain in preparation for the final step of the psychoacoustic model, the calculation of the signal-to-mask ratios (SMR) for each subband. Figure 14b is a plot of these results and figure 14c is a frequency plot of a processed audio signal using these SMR’s. In this example the audio compression was severe (768 to 64 kbits/sec) so the coder may not necessarily be able to mask all the quantization noise.

The Psychoacoustic Model

The psychoacoustic model calculates just-noticeable distortion (JND) profiles for each band in the filterbank. This noise level is used to determine the actual quantizers and quantizer levels. There are two psychoacoustic models defined by the standard. They can be applied to any layer of the MPEG/Audio algorithm. In practice however, Model 1 has been used for Layers I and II and Model 2 for Layer III. Both models compute a signal-to- mask ratio (SMR) for each band (Layers I and II) or group of bands (Layer III).

The more sophisticated of the two, Model 2, will be discussed. The steps leading to the computation of the JND profiles is outlined below. 1. Time-align audio data

The psychoacoustic model must estimate the masking thresholds for the audio data that are to be quantized. So, it must account for both the delay through the filterbank and a data offset so that the relevant data is centered within the psychoacoustic analysis window. For the Layer III algorithm, time-aligning the psychoacoustic model with the filterbank demands that the data fed to the model be delayed by 768 samples. 2. Spectral analysis and normalization.

A high-resolution spectral estimate of the time-aligned data is essential for an accurate estimation of the masking thresholds in the critical bands. The low frequency resolution of the filterbank leaves no option but to compute an independent time-to-frequency mapping via a fast Fourier Transform (FFT). A Hanning window is applied to the data to reduce the edge effects of the transform window.

Layer III operates on 1152-sample data frames. Model 2 uses a 1024- point window for spectral estimation. Ideally, the analysis window should completely cover the samples to be coded. The model computes two 1024-point psychoacoustic calculations. On the first pass, the first 576 samples are centered in the analysis window. The second pass centers the remaining samples. The model combines the results of the two calculations by using the more stringent of the two JND estimates for bit or noise allocation in each subband.

Since playback levels are unknown3, the sound-pressure level (SPL) needs to be normalized. This implies clamping the lowest point in the absolute threshold of hearing curves to +/- 1-bit amplitude. 3. Grouping of spectral values into threshold calculation partitions.

The uniform frequency decomposition and poor selectivity of the filterbank do not reflect the response of the BM. To accurately model the masking phenomenon characteristic of the BM, the spectral values are grouped into a large number of partitions. The exact number of threshold partitions depends on the choice of sampling rate. This transformation provides a resolution of approximately either 1 FFT line or 1/3 critical band, whichever is smaller. At low frequencies, a single line of the FFT will constitute a partition, while at high frequencies many lines are grouped into one. 4. Estimation of tonality indices.

It is necessary to identify tonal and non-tonal (noise-like) components because the masking abilities of the two types of signals differ. Model 2 does not explicitly separate tonal and non-tonal components[16]. Instead, it computes a tonality index as a function of frequency. This is an indicator of the tone-like or noise-like nature of the spectral component. The tonality index is based on a measure of predictability. Linear extrapolation is used to predict the component values of the current window from the previous two analysis windows. Model 2 uses this index to interpolate between pure tone-masking-noise and noise-masking-tone values. Tonal components are more predictable and thus have a higher tonality index. As this process has memory, it is more likely to discriminate better between tonal and non-tonal components, unlike psychoacoustic Model 116. 5. Simulation of the spread of masking on the BM.

A strong signal component affects the audibility of weaker components in the same critical band and the adjacent bands. Model 2 simulates this phenomenon by applying a Spreading function to spread the energy of any critical band into its surrounding bands. On the Bark scale, the spreading function has a constant shape as a function of partition number, with slopes of +25 and –10 dB per Bark. 6. Set a lower bound for the threshold values.

An empirically determined absolute masking threshold, the threshold in quiet, is used as a lower bound on the audibility of sound. 7. Determination of masking threshold per subband.

At low frequencies, the minimum of the masking thresholds within a subband is chosen as the threshold value. At higher frequencies, the average of the thresholds within the subband is selected as the masking threshold. Model 2 has the same accuracy for the higher subbands as for low frequency ones because it does not concentrate non-tonal components16. 8. Pre echo detection and window switching decision[17]?. 9. Calculation of the signal-to-mask ratio (SMR).

SMR is calculated as a ratio of signal energy within the subband (for Layers I and II) or a group of subbands (Layer III) to the minimum threshold for that subband. This is the final output of the psychoacoustic model.

The masking threshold computed from the spread energy and the tonality index.

Processes in the psychoacoustic model

Performs a 1024-sample FFTs on each half of a frame (1152 samples) of the input signal, selecting the lower of the two masking thresholds to use for that subband.

Each frequency bin is mapped to its corresponding critical band.

Calculate a tonality index, a measure of whether a signal is more tone-like or noise-like.

Use a defined spreading function to calculate the masking effect of the signal on neighbouring critical bands.

Calculate the final masking threshold for each subband, using the tonality index, the output of the spreading function, and the ATH.

Calculate the signal-to-mask ratio for each subband, and passes information on to the quantizer.