Sliding DFT: Difference between revisions
mNo edit summary |
(Added image(s)) |
||
| Line 1: | Line 1: | ||
{{Stub}} | {{Stub}} | ||
[[Image:sDFT network.png|thumb|A block diagram of guaranteed-stable sDFT network with non-integer K.]] | |||
A '''sliding [[DFT]]''' is a recursive complex FIR filter bank that calculates short-time Fourier transform sample-by-sample. Unlike [[FFT]], the sDFT calculation for each bin is independent of each other, making it ideal for single-bin STFT and even [[constant-Q transform]] but this technique are limited by having only integer K otherwise, the sDFT goes out of phase but this is not in case on some sDFT implementations that allows non-integer K.<ref>The section "Sliding Spectrum Analysis for a Non-integer k Analysis Frequency" at "[https://digital.library.adelaide.edu.au/dspace/bitstream/2440/133370/3/hdl_133370.pdf Improvements to the Sliding DFT Algorithm]" by Richard Lyons and Carl Howard (July 2021)</ref> | A '''sliding [[DFT]]''' is a recursive complex FIR filter bank that calculates short-time Fourier transform sample-by-sample. Unlike [[FFT]], the sDFT calculation for each bin is independent of each other, making it ideal for single-bin STFT and even [[constant-Q transform]] but this technique are limited by having only integer K otherwise, the sDFT goes out of phase but this is not in case on some sDFT implementations that allows non-integer K.<ref>The section "Sliding Spectrum Analysis for a Non-integer k Analysis Frequency" at "[https://digital.library.adelaide.edu.au/dspace/bitstream/2440/133370/3/hdl_133370.pdf Improvements to the Sliding DFT Algorithm]" by Richard Lyons and Carl Howard (July 2021)</ref> | ||
Revision as of 21:03, 15 June 2023
This article is a stub. You can help the Hydrogenaudio Knowledgebase by expanding it.
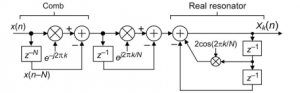
A sliding DFT is a recursive complex FIR filter bank that calculates short-time Fourier transform sample-by-sample. Unlike FFT, the sDFT calculation for each bin is independent of each other, making it ideal for single-bin STFT and even constant-Q transform but this technique are limited by having only integer K otherwise, the sDFT goes out of phase but this is not in case on some sDFT implementations that allows non-integer K.[1]
The sliding DFT can also have asymmetric windowing function by replacing ring buffers with an IIR exponential decay and it can be cascaded to further increase rolloff.[2][3]
Implementation in foobar2000
The sliding DFT, unlike FFT requires contiguous stream of data, which means implementing that requires tricks involved with delta variable (time difference between current and previous calculations). However, the offset part of audio capture part of visualization (especially with get_chunk_absolute(data, offset, size)) is kinda complicated; the time of the resulting captured signal is requested_length/2 samples ahead of actual playback (as long as the requested length is lower than buffer size in samples), which means the offset should be adjusted to something like time - delta/2.
References
- ↑ The section "Sliding Spectrum Analysis for a Non-integer k Analysis Frequency" at "Improvements to the Sliding DFT Algorithm" by Richard Lyons and Carl Howard (July 2021)
- ↑ A paper "The Sliding Windowed Infinite Fourier Transform" on "Tips & Tricks" part of IEEE Signal Processing Magazine
- ↑ Implementation of the sliding windowed infinite Fourier transform with functionality to cascade sDFTs serially at GitHub Gist
