Modified Discrete Cosine Transform: Difference between revisions
No edit summary |
No edit summary |
||
| Line 25: | Line 25: | ||
* [http://www.comp.nus.edu.sg/~wangye/publications/Conference%20papers/00027_aes22.pdf Modified Discrete Cosine Transform] a complete research paper on MDCT presented at the 22nd AES conference. | * [http://www.comp.nus.edu.sg/~wangye/publications/Conference%20papers/00027_aes22.pdf Modified Discrete Cosine Transform] a complete research paper on MDCT presented at the 22nd AES conference. | ||
[[Category:Algorithms]] | |||
[[Category: | |||
Revision as of 22:39, 7 September 2006
This article is a stub. You can help the Hydrogenaudio Knowledgebase by expanding it.
The MDCT (Modified Discrete Cosine Transform) is a DCT-IV transform. The MDCT tries to minimize blocking artifacts. It is common in lossy audio codecs including MP3, Vorbis, and AAC.
As a lapped transform, the MDCT is a bit unusual compared to other Fourier-related transforms in that it has half as many outputs as inputs (instead of the same number). In particular, it is a linear function F : R2n -> Rn (where R denotes the set of real numbers). The 2n real numbers x0, ..., x2n-1 are transformed into the n real numbers f0, ..., fn-1 according to the formula:
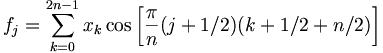
The inverse MDCT is known as the IMDCT. Because there are different numbers of inputs and outputs, at first glance it might seem that the MDCT should not be invertible. However, perfect invertibility is achieved by adding the overlapped IMDCTs of subsequent overlapping blocks, causing the errors to cancel and the original data to be retrieved; this technique is known as time-domain aliasing cancellation (TDAC).
The IMDCT transforms n real numbers f0, ..., fn-1 into 2n real numbers y0, ..., y2n-1 according to the formula:
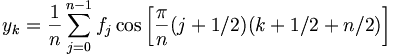
The MDCT was developed by Henrique Malvar, and engineer now working for Microsoft and that had considerable participation in creating the WMA format.
References
- Discrete Fourier Transform it's basic properties and applications.
- Planet CCRMA description of the DCT-IV.
- Modified Discrete Cosine Transform a complete research paper on MDCT presented at the 22nd AES conference.
