Finite Impulse Response Filter
Finite impulse response (FIR) filters are digital filters carried out by convolution.
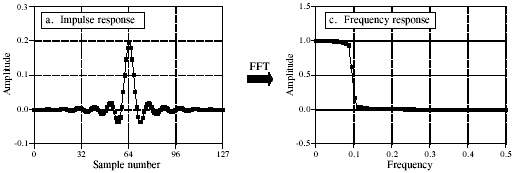
The most straightforward way to implement a digital filter is by convolving the input signal with the digital filter's impulse response (Impulse here in digital signal processing means a pulse with a single nonzero sample). Digital filter's Impulse response is also called a filter kernel.
To implement the fir filter, an input signal x(n) is convolved with fir filter's impulse response h(n), resulting in a filtered output signal y(n). The output signal from a linear system (from our fir filter) is equal to the input signal convolved with the filter's impulse response. the operation (x)*(h) is called convolution.
Convolution is a formal mathematical operation in signal processing: 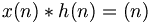 although the star does not imply multiplication, instead it implies the convolution process. The resulting filtered signal's frequency response (frequency response of y(n)) follows the shape of filter's frequency response (figure above).
although the star does not imply multiplication, instead it implies the convolution process. The resulting filtered signal's frequency response (frequency response of y(n)) follows the shape of filter's frequency response (figure above).
When a filter is implemented by convolution, each sample in the output is calculated by weighting the samples in the input, and adding them together. Recursive filters (iir; infinite impulse response) are an extension of this, using previously calculated values from the output, besides points from the input.
See also
- Infinite Impulse Response Filter (IIR filter)