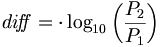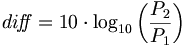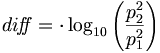Difference between revisions of "Bel"
(hope my adjustments are right) |
m |
||
| Line 5: | Line 5: | ||
::<math>{di\! f\!\! f} = \cdot \log_{10}\left(\frac{P_2}{P_1}\right )</math> | ::<math>{di\! f\!\! f} = \cdot \log_{10}\left(\frac{P_2}{P_1}\right )</math> | ||
| − | In case of the | + | In case of the ''deci''bel we have a ''10'' factor: |
::<math>{di\! f\!\! f} = 10 \cdot \log_{10}\left(\frac{P_2}{P_1}\right )</math> | ::<math>{di\! f\!\! f} = 10 \cdot \log_{10}\left(\frac{P_2}{P_1}\right )</math> | ||
Latest revision as of 17:53, 14 June 2007
The bel (B) is a logarithmical unit used to express relative difference in intensity or power between two signals, usually acoustic. Because of the fact that the Bel unit is too large for everyday use most of the times it is used as the more convenient decibel (abbreviated to dB).
Decibel is equal to ten times the common logarithm of the ratio of the two levels.
In case of the decibel we have a 10 factor:
There is a second definition of the decibel. In acoustics, it is used to express the ratio in sound pressure, because power is roughly proportional to the square of effective sound pressure.
Let 'p' be pressure, 'P' power.
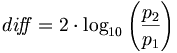 because
because 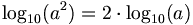
In this scale, it means an increase of 20 B is equal to a ten-fold ratio, or 6 B a two-fold ratio (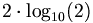 is approximately equal to 6).
is approximately equal to 6).